今天做题，偶遇Dijkstra，记录下来
Dijkstra算法由计算机科学家Edsger Dijkstra在1956年提出。该算法适用于有向图和无向图，且图中的边权重必须为非负数。
算法理解
假设有如下图，我们需要计算从A到D的最短路径

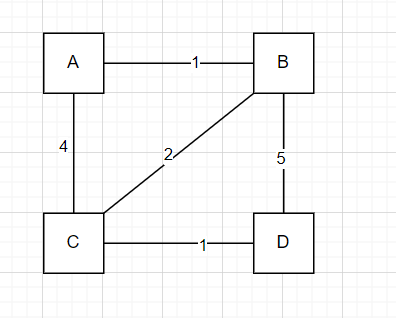
我们用一个数组记录A到所有节点的距离[]

1. 第一步初始化，到自己为0，到其他节点为无穷， 所以得到 [0, ∞， ∞， ∞]
2. 第二步计算A直接相连节点，更新A到所有节点的距离，得到 [0, 1，4，∞]
3. 第三步移到节点B， 计算B直接相连的，更新A到所有节点的距离，得到 [0, 1，3，6]
4. 第四步移到节点C， 计算C直接相连的距离，更新A到所有节点的距离，得到 [0, 1，3，4]
5. D是最后一个节点，不需要计算了~

所以我们就得到了A 到其他节点的最短路径

强调一下：所有边的权重非负，因为负的权重会破坏数组是已知节点的最优解（比如重复走负权重这条路会让总距离越来越短~）

实际应用场景举例：

1. 地图导航-计算最短/最快路径
2. 网络数据包路由
3. 物流运输
4. 社交网络-找朋友
5. 电力/交通系统规划

如果权重为负，比如计算最小成本的时候，某些路径上出现了收益…

下一篇介绍Bellman-Ford算法来正确处理负权重的问题。