听了8节免费课，感觉懂了点，又感觉没懂！先记下来

什么是深度学习 – 深度神经网络的权重参数学习

从系统论来看，万事万物可以看成下面的基础结构（多层感知机）

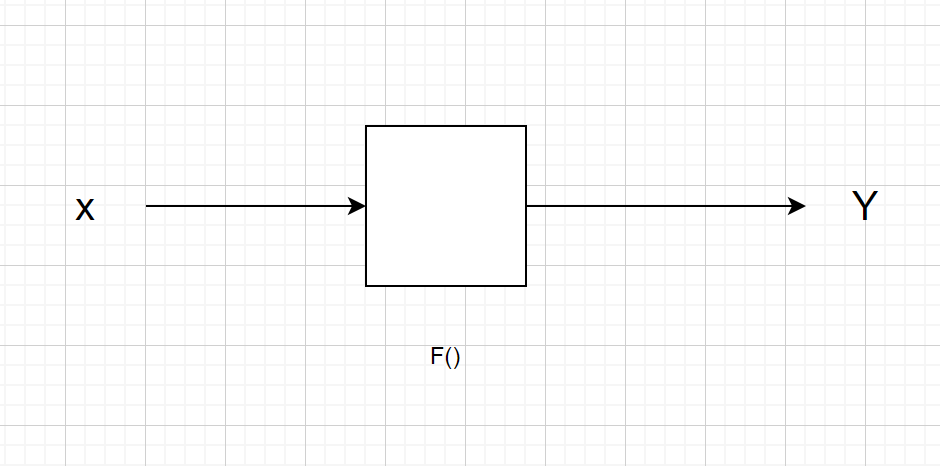
从 Y = f(Wx + b)
到 Y = fnfn-1…fo(Wx + b)

深度学习就是 求这个W
深度就是线性模型外面套激活函数，一层一层来逼近目标

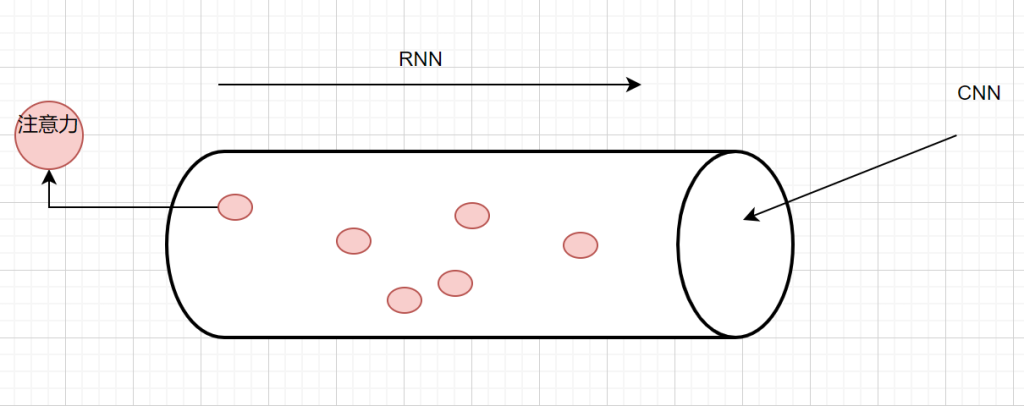
CNN，卷积神经网络->空间维度的一个截面- 把W通过w卷积

RNN：循环神经网络 -> 考虑时间/时序维度的关系

Yn = f（Ux + WYn-1 + B ）

注意力网络： Transformer -> 认知科学维度，聚焦关键特征

Y = softmax(QK / [d])V

AIGC

机器视觉 CV

语音

NLP – 文本，以及背后的语义，逻辑，情感，意图等 -> LLM -> AI2.0

多模态 – 多媒体 – 文本，图形，视频，语音的生成和交互

线性代数 – 数据表达 – 前向传播

概率统计 – 损失函数 – 优化引擎

微积分 -链式法则- 反向传播

向量和矩阵：数据在AI领域的数字表达
神经网络的核心操作是线性变换 + 非线性激活，就是前面讲的：输入向量 x 通过权重矩阵 W 完成线性变换 y=Wx+b

卷积神经网络（CNN）中的卷积操作可视为稀疏矩阵乘法，利用局部连接和权值共享减少计算量

AI 模型（如神经网络）通过损失函数（如交叉熵）衡量预测误差，需利用微积分中的导数找到使损失最小的参数。
梯度（Gradient）是损失函数对参数的偏导数向量，指引参数更新的方向（沿梯度反方向更新可最快降低损失）

反向传播算法（Backpropagation）本质是链式法则的应用，递归计算每个参数的梯度，实现端到端的优化。

动量法（Momentum）引入梯度的一阶惯性（类似物理中的动量），通过指数加权平均加速收敛；

Adam 算法结合梯度的一阶矩（均值）和二阶矩（方差），自适应调整学习率，其推导依赖泰勒展开、牛顿法等微积分理论。

为了使用梯度下降优化，激活函数（如 ReLU、Sigmoid、Tanh）必须可导（或近似可导）。

微积分支持对连续变量的建模（如回归问题预测房价、温度等连续值），而离散优化（如组合问题）常通过连续松弛（如将 0-1 变量松弛为 [0,1] 区间的实数）转化为微积分问题求解。

分类模型通过 Sigmoid 函数将线性变换结果映射为概率（如二分类中 \(P(y=1|X) = \sigma(\mathbf{w}^T\mathbf{x})\)），损失函数（交叉熵）对应极大似然估计的优化目标

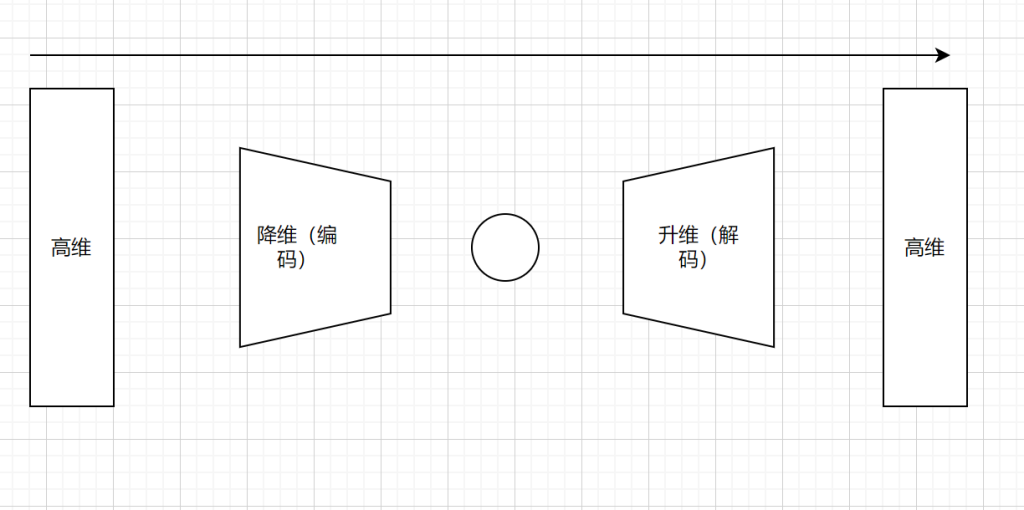
生成模型变分自编码器（VAE）假设隐变量 z 服从先验分布（如标准正态分布），通过编码器 \(q(z|X)\) 近似后验分布 \(p(z|X)\)，解码器 \(p(X|z)\) 生成新样本，目标是最大化对数似然的变分下界

归一化流（Normalizing Flow）通过可逆变换将简单分布（如高斯分布）转化为复杂数据分布，利用概率密度变换公式（雅可比行列式）计算似然

多头注意力机制（Multi-Head Attention）通过线性变换（矩阵乘法）将查询（Query）、键（Key）、值（Value）映射到多个子空间，计算注意力权重时使用点积（内积）和 Softmax 函数（归一化概率分布）

位置编码（Positional Encoding）利用正弦余弦函数（微积分中的周期函数）引入序列顺序信息，避免纯线性变换的排列不变性

总结：微积分中的链式法则支撑反向传播算法，而线性代数中的矩阵求导（如雅可比矩阵、海森矩阵）提供参数梯度的计算框架，概率论中的期望运算（如损失函数的数学期望）将样本层面的优化扩展到总体分布。